POLJE

pojam, podela, matemat. alati
tajanstvo prostora i pojava u njemu - na tzv. naučni način

           Pojam polja  

Bilo kakav prostor čini skup tačaka. Tačka je beskrajno mali deo prostora uopšte, osnovni element.

Složeniji elementi mogu biti:

◦ niz tačaka jedna do druge čine liniju. Gde se razlikuje prava linija od krive linije.
  Prava linija se kraće zove samo prava.

◦ niz pravih, poređanih paraleleno jedna do druge, čine ravan.

◦ niz ravni, paralelno poređanih jedna do druge, čine naš tro-dimenzionalni prostor.

Dakle postoje 4 stepena geneze prostora: tačka, linija(prava), ravan i prostor kao takav. Ovaj prostor je nama, našim čulima lako razumljiv zahvaljujući hiljadama i hiljadama godina iskustva bivstvovanja u njemu.
Radi lakšeg razumevanja pogledajmo šta se sve pojavilo (na Zemnlji) za svo to vreme našeg bivstvovanja. Na zemlji postoje, takođe 4 vrste organizovane materije: minerali, biljke, životinje i ljudi. Nama svima je lako da zamislimo, a u člancima po novinama svi zamišljamo, jasno i lako neka nova, buduća 'ljudska' stvorenja.
Dakle 5-tu vrstu organizovane materije.

Obrnuto 5-tu vrstu 'prostora' ili kako bi ga već zvali, naš pojmovni aparat teško može da predstavi ili vizualizuje. Da bi se ipak nekako 'suočili' sa ovakvim pojmom koristi se matematički aparat.
Koriste se uski i apstraktni oblici ljudskog uma. Ovi su samo delimično slikoviti, a ostatak se posmatra samo po analogiji.

Tačka je manja i od najmanjeg otiska, najoštrije olovke na papiru. Manja je i od najmanje čestice prašine pod zrakom sunčeve svetlosti.
Dakle tačka je ispod praga čulnog doživljaja! I odavde počinju sve nedoumice "šta matematički zaključci znače"?
Između 1 nacrtane tačke i tačke po definiciji - postoje milioni-milijarde vasiona i kosmosa različitih dimenzija.
Kada svakoj tački, bilo koliko ili bilo kako organizovanih tačaka pridružimo jedan ili više brojeva dobijamo tzv. polje.

Polje je skup tačaka kojima je prirdruženo jedan ili više brojeva.
Niz veza između broja i pojedine tačke čini zajedno funkciju Φ.

Svaka tačka se imenuje jenim slovom latinice, na pr. M. Svaka osoba se imenuje nekim imenonm, na pr. M. Da bi odredili o kojoj osobi je reč treba da znamo: najmanje grad u kome živi, dalje barem ulicu gde stanuje a najzad i sam broj kuće.
Slično je i sa svim tačkama. Za bliže određivanje, o kojoj tački je reč određujemo:

najmanje jedan niz refrentnih tačaka = koordinatna osa imenom x-osa .
    prva tačka niza je koordinatni početak - Ox
    kažemo da je to jednodimenzionalna zavisnost, duž jedne linije M(x);

za preciznije određivanje sa dva niza refrentnih tačaka = 2 koordinatne ose imenom x-osa i y-osa.
    prve tačke niza su koordinatni početak - Ox i Oy
    kažemo da je to dvodimenzionalna zavisnost, duž jedne ravni M(x,y);

kompletan obuhvat sa tri niza refrentnih tačaka = 3 koordinatne ose imenom x-osa, y-osa i z-osa.
    prve tačke niza su koordinatni početak - Ox, Oy i Oz
    kažemo da je to trodimenzionalna zavisnost, u prostoru M(x,y,z)

Sa obuhvatom M(x,y,z) se završava naša mentalna i čulima dostupna okolna stvarnost. Sve ostalo su formalne konstrukcije i modeli prostora.

Moguća predpostavka je i "a gde je 4-ti niz tačaka, 4-ta koordinara!?"

kompletan obuhvat sa četiri niza refrentnih tačaka = 4 koordinatne ose imenom x-osa, y-osa i z-osa i t-osa.
    prve tačke niza su koordinatni početak - Ox, Oy, Oz i Ot
    kažemo da je to četvorodimenzionalna zavisnost, u mega-prostoru M(x,y,z,t)

više o 4-toj koordinati, pogledaj na: ›››

_____________________________
napomena: Fizičari znaju da su modeli matematičke konstrukcije koje 'pokrivaju' neki proces-događaj u stvarnosti. Svaki tzv. ulaz i izlaz u toku odvijanja nekog procesa-događaja je povezan tzv. "cnom kutijom". Eksperimentator nikad nezna šta se tačno dešava u "crnoj kutiji"! On samo pokušava da nasluti dubinu i složenost niza događaja koji čine zadati proces-događaj. Svaka hipoteza, 'teorija' je samo još jedan model.

Majbolji model (teorija) uspostavlja maksimalno dobro poklapanje ulaza i izlaza realnog događaja (crne kutije) i osmišljenog modela. Isto tako svaki dobar model sadrži predhodni model kao svoj specijalni slučaj. Svaki model sa potpuno novom paradigmom, koji ne sadrži predhodne slučajeve kao svoj deo, u praksi nema veće značenje.
_____________________________
napomena: Svaki proces-događaj karakterišu neke veličine koje, po definiciji, mogu da rastu ili da opadaju. One mogu da se predstave merenim brojevima u odgovarajučim jedinicama (const. veličina istog tipa).
    skalari su veličine kojima se pridružuje samo 1 broj (masa u [kg], temperatura u [°K], kol. elektriciteta u [C] itd.).
    vektori su veličine koje čine 3 druge veličine (3 skalara): intenzitet brojna vrednost, pravac prava linija i smer orijentacija duž prave.



           Skalarno polje  

Kada postoji mnoštvo tačaka M_i ( i=1,2,3,4. . . . ∞ ) i svakoj tački pridružimo jedan broj Φ_i (skalar) tada nastaje polje.

skalarno polje nastaje kada svakoj tačaki skupa dodelimo niz pojedinačnih vrednosti skalara.
Sve veze brojnih vrednosti skalara i odgovarajuće tačke definiše funkciju skalarnog polja Φ

Skup tačaka može biti:
      na jednoj liniji (bilo prava, bilo kriva) M(x) - jednodienziono polje,
      na jednoj površini (ravnoj) M(x,y) - dvodimenziono polje, i
      na jednoj površi (krivoj) ili u prostoru M(x,y,z) - trodimenziono polje.


Posmatramo tačku M(x,y) u ravni, kojoj pripada vrednost funkcije Φ(x,y). Neka funkcija ima neprekidne parcijalne izvode prvog reda. Dalje u tački M₀(x₀,y₀) funkcija Φ(x₀,y₀) ima vrednost, pridruženi broj c.
Postavljamo dva matematička uslova:

Φ(x₀,y₀) = c i ako važi
Φ_x^'2(x₀,y₀)+Φ_y^'2(x₀,y₀) ≠ 0

Jdnačinom Φ(x,y)=c definisana je neka glatka kriva u okolini i kroz tačku M₀.
Ovo je nivo-linija skalarnog polja.
U svakoj tački nivo-linije funkcija Φ(x,y) ima istu (const.) vrednost,
pa se zato još i zovu akviskalarne linije.

stacionarne tačke skalarnog polja su u tačkama u gde su Φ_x^'=0 i Φ_y^'=0, odnosno drugi uslov Φ_x^'2(x₀,y₀)+Φ_y^'2(x₀,y₀)+ ≠ 0 nije ispunjen.
singularne tačke nivo-linija su izolovane tačke ili lukovi linija gde nije ispinjen drugi uslov.
U svim tačkama skalarnog polja gde gfunkcija Φ(x,y) ima neprestano istu vrednost definiše se homogeno skalarno polje.

Kada u nekom otvorenom području ravni Oxy nema oblasti u kojima je Φ(x,y)=const. i nema stacionarnih tačaka, tada kroz svaku tačku prolazi jedna i samo jedna nivo-linija.

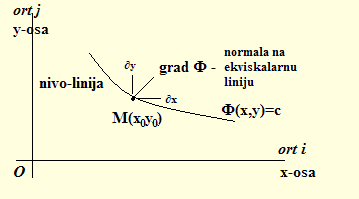
kako su: Φx' = ∂Φ   priraštaj f-je Δx -> 0 za y=const. dakle duž paralelena x-osi ∂x Φy' = ∂Φ   priraštaj f-je Δy -> 0 za x=const. dakle duž paralelena y-osi ∂y sledi: Φx' ┴ Φy' su ortogonalne duži a (Φx'2 + Φy'2)½ je hipotenuza pravouglog trougla i normala na ekviskalarnu krivu u Oxy ravni

_____________________________
napomena: ort je vektor intenziteta 1, jedinični vektor, koji def. neki pravac i smer.
Množenjem ort-a nekim skalarom λ dobija se vektor unapred određenog pravca i smera.

Za lakši prikaz koordinatnih osa koriste se: ort i, ort j, ort k, jedinični vektori koji određuju pravac i smer pojedinih koordinatnih osa, a za koje važe zakoni vektorskog množenja:
skalarno množenje:
       i • i = 1; j • j = 1, k • k = 1
       a svi ostali   i • j; i • k; j • i; j • k; k • i; k • j = 0 su jednaki nuli (ortogonalni vektori)
vektorsko množenje:
       i × i = 0 ;  i × j = k ;  i × k = -j
       j × i =-k ;  j × j = 0 ;  j × k = i
       k × i = j ,  k × j = -i ;  k × k = 0

Kako je Φ_x^' veličina paralelna sa x-osom, množenjem sa ortom-i parcijalni izvod postaje vektor paralelan x-osi!
Dalje je Φ_y^' veličina paralelna sa y-osom, množenjem sa ortom-j parcijalni izvod postaje vektor paralelan y-osi!
normala na nivo-liniju postaje vektor i dobija naziv grad Φ. Ovaj gradijent se dobija kao vektorski zbir:

grad Φ(x,y) = (Φx')i + (Φy')j =

∂Φ i ∂x

+

∂Φ j ∂y

kako su: dx   priraštaj f-je Δs -> ds u pravcu x-ose (ort i) ds dy   priraštaj f-je Δs -> ds u pravcu y-ose (ort j) ds sledi da je ort tangente: t0 = dx i + dy j ds ds

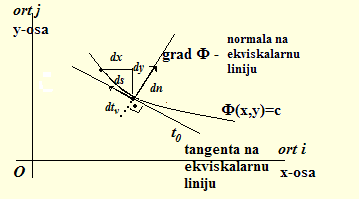
Priraštaj f-je dΦ u pravcu luka ds daje:

dΦ

=

∂Φ

·

dx

+

∂Φ

·

dy

dalje je to   skalarni proizvod dva vektora

dΦ

= ﴾

dx

i +

dy

j ﴿ • ﴾

∂Φ

i +

∂Φ

j ﴿

ili jednostavnije   pomoću vektora

dΦ

= t0 • grad Φ

ds

∂x

ds

∂y

ds

ds

ds

ds

∂x

∂y

ds

Samo priraštaj f-je dΦ nastaje množenjem sa ds: dΦ = ds·t₀ • grad Φ
ds·t₀ = dt_v dakle vektor u u pravcu tangente
dΦ = dt_v • grad Φ
skalarni proizvod vektora u pravcu tangente i vektora gradijenta Priraštaj f-je u pravcu luka ekviskalarne linije Φ(x,y)=const. ne postoji, on je nula dΦ=0! dt_v • grad Φ = 0

dt_v ┴ grad Φ = 0
vektor grad Φ je upravan na vektor tangente
(skalrni proizvod je nula)
uvek ima pravac normale na ekviskalarnu linju f-je Φ(x,y)=const.

Priraštaj f-je dΦ u pravcu normale dn na ekviskalarnu liniju daje:

dΦ

=

∂Φ

·

dx

+

∂Φ

·

dy

dalje je to   skalarni proizvod dva vektora

dΦ

= ﴾

dx

i +

dy

j ﴿ • ﴾

∂Φ

i +

∂Φ

j ﴿

ili jednostavnije   pomoću vektora

dΦ

= n0 • grad Φ

dn

∂x

dn

∂y

dn

dn

dn

dn

∂x

∂y

dn

n₀ • grad Φ = | grad Φ |   ( skalarni proizvod = brojna vrednost, intenzitet )
intenzitet gradijenta ima vrednost izvoda skalara u pravcu n₀ normale na ekviskalarnu liniju

Priraštaj dΦ f-je u pravcu normale dn na ekviskalarnu liniju dΦ = dn · (n₀ • grad Φ)
uvek ima vrednost u smeru rasta f-je Φ

dΦ > 0  =>  n₀ • grad Φ > 0
grad Φ uvek ima smer rasta skalarne f-je Φ(x,y)

---

Izborom tačke M(x,y,z) u prostoru, kojo pripada funkcija Φ(x,y,z) proširujemo pojam skalarnog polja sa istim uslovima kao u predhodnom slučaju. Neka funkcija ima neprekidne parcijalne izvode prvog reda. Dalje u tački M₀(x₀,y₀,z₀) funkcija Φ(x₀,y₀,z₀) ima vrednost, pridruženi broj c.
Takođe važi:

Φ(x,y,z) = c i ako važi
Φ_x^'2(x,y,z)+Φ_y^'2(x,y,z)+Φ_z^'2(x,y,z) ≠ 0

Jdnačinom Φ(x,y,z)=c definisana je neka glatka površina u okolini i kroz tačku M₀.
Ovo je nivo-površina trodimenzionog skalarnog polja.
U svakoj tački nivo-površine funkcija Φ(x,y,z) ima istu (const.) vrednost,
pa se zato još i zove ekviskalarna površina.

stacionarne tačke skalarnog polja su u tačkama u gde su Φ_x^'=0, Φ_y^'=0 i Φ_z^'=0, odnosno drugi uslov Φ_x^'2(x,y,z)+Φ_y^'2(x,y,z)+Φ_z^'2(x,y,z) ≠ 0 nije ispunjen.
singularne tačke nivo-površina su izolovane tačke, lukovi ili površine gde nije ispinjen drugi uslov.
U svim tačkama skalarnog polja gde gfunkcija Φ(x,y,z) ima neprestano istu vrednost definiše se homogeno skalarno polje.

Kada u nekom otvorenom području ravni Oxy nema oblasti u kojima je Φ(x,y)=const. i nema stacionarnih tačaka, tada kroz svaku tačku prolazi jedna i samo jedna nivo-površina.

Za gradijent f-je Φ(x,y,z) postoje anlogni izrazi u prostoru:

grad Φ(x,y,z) =

∂Φ i ∂x

+

∂Φ j ∂y

+

∂Φ k ∂z

uvek ima pravac normale na ekviskalarnu površ f-je Φ(x,y,z)=const.
intenzitet gradijenta ima vrednost izvoda skalara u pravcu n₀ normale na ekviskalarnu površ.
grad Φ uvek ima smer rasta skalarne f-je Φ(x,y,z).

           Vektorsko polje  

Na ovaj način skalarno polje ima samo 2 'alata' za analizu proces-događaj-a:
     - ekviskalarne površi f-je Φ(x,y,z)=c i
     - gradijent Φ - pravac i smer rasta f-je Φ(x,y,z).

Da bi se obuhvatilo što više događaja i situacija dinamički treba znati i šire veličine, a to je proizvoljan, bilo koji pravac i smer razvoja procesa-događaja!

Zato je potrebno da znamo početnu tačku M(x,y,z) i krajnju tačku M₁(x,y,z), dalje njihovu prostornu orijentaciju - duž MM₁.
Ovakav složeniji obuhvat skalarnog polja zahteva odgovarajuće 'duži' u pravcu svake od osa i, j, k dakle neke f-je:
      Φ₁(x,y,z) - u pravcu x-ose (ort i)
      Φ₂(x,y,z) - u pravcu y-ose (ort j)
      Φ₃(x,y,z) - u pravcu z-ose (ort k)
Očigledno da bi trebalo da se prate 3 skalarna polja sinhrono!
Rešenje je uvođenje 1 (jedne) vektorske funkcije: Φ_v( r ) = Φ₁(x,y,z) i + Φ₂(x,y,z) j + Φ₃(x,y,z) k

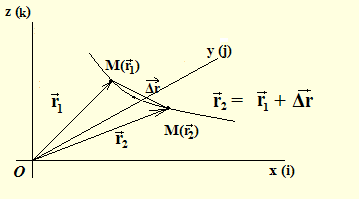
Svaku tačku u vektorskom polju određuje vektor poližaja rv, radijus vektor. Prostorni pomeraj je tada: Δr = r2 − r1 (razlika vektora) dr = dx i + dy j + dz k

Veza između skalarnog- i vektorskog-polja se vidi kad se skalarna veličina grad Φ(x,y,z) trodimenzionalnog skalrnog polja kostituiše kao vektor.
Ako sa g_v (r) označimo grad Φ kao vektor:

gv(r) =	∂Φ	i +	∂Φ	j +	∂Φ	k
	∂x		∂y		∂z

biće i skalarni proizvod vektora g_v(r) i dr orijentisani element gradijenta:

gv(r) • dr = ﴾	∂Φ	i +	∂Φ	j +	∂Φ	k ﴿ • ﴾ dx i + dy j + dz k ﴿
	∂x		∂y		∂z
=	∂Φ	dx +	∂Φ	dy +	∂Φ	dz = ΔΦ
	∂x		∂y		∂z

zapravo priraštaj ΔΦ skalarne funkcije.

gradijentsko polje čini specijalno vektorsko polje trodimenzionalnog skalarnog polja definisanog f-jom Φ(x,y,z).
Funkcija Φ(x,y,z) je potencijal tog polja, pa se zato i gradijentsko polje zove i potencijalno polje.

Ako u tački M₀(x,y,z) postoji usmeren proces-događaj, tu onda postoji i vektor  v_v^*(x,y,z), koji se slobodno formira iz tačke M₀ do tačke M₁.
Vektor v_v^* ima i 3 komponente v₁(x,y,z), v₂(x,y,z), v₃(x,y,z), sa početkom u M₀.
Tačka M₀(x,y,z) se određuje radijus vektorom r_v^*(x,y,z) iz koordinartnog početka M(0,0,0).
Odatle proističu i sledeći matemat. objekti i veličine:

---

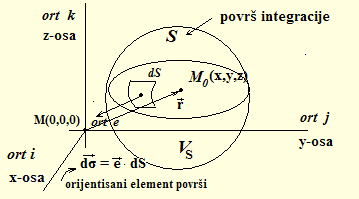
*napomena: index-v ( vv; rv; drv; ev; dσv; ) se stavlja umesto vektorske strelice iznad slova!

prosti, osnovni elementi:       drv* - orijentisani element krive linije       ev*=e1 i + e2 j + e3 k    je ort normale na površ integracije       dσv* = ev · dS   je orijentisan element površi       S - je površ integracije       VS - je prostorni, zapreminski obuhvat površine S       Ip = ∫ S  φ(rv*) • dσv    je površinski integral f-je položaja       funkcija φ(rv) je skalarna funkcija položaja a može biti i       funkcija φ(rv) = vv (rv) vektorska funkcija položaja

---

i složeni elementi:

lim	Ip	=  prostorni izvod f-je φ(rv)
VS → 0	VS

Uz prostorni izvod slede i neke standardfne matemat. forme:

1° ▼ - nabla ili Hamiltonov operator        (formalni, simbolički operator)	▼ =	∂	i +	∂	j +	∂	k
		∂x		∂y		∂z
2° Δ =▼•▼= ▼2 - Laplasov operator	Δ =	∂2	+	∂2	+	∂2
		∂x2		∂y2		∂z2

3° Formula Ostrogradskog (Gaus-Ostrogradski) povezuje f-je P, Q, R kao podintegralne izraze
∫ po proizvoljnoj površi dS i ∫ po njome zahvaćenom zapreminom dV

∫

S Pdydz + Qdzdx + Rdxdy =

∫

VS ﴾

∂P

+

∂Q

+

∂R

﴿ dxdydz

ili drugačije    po dS i dV

∫

S ﴾ Pe1 + Qe2 + Re3 ﴿ dS =

∫

VS ﴾

∂P

+

∂Q

+

∂R

﴿ dV

∂x

∂y

∂z

∂x

∂y

∂z

Ako su f-je P=v₁(x,y,z), Q=v₂(x,y,z) i R=v₃(x,y,z) onda iz gornje formule Ostrogradskog biće:

∫

S ﴾ v1e1 + v2e2 + v3e3 ﴿ dS =

∫

S vv • edS =

∫

S vv • dσv =

∫

VS ﴾

∂v1

+

∂v2

+

∂v3

﴿ dV

∂x

∂y

∂z

4° Stoksova formula povezuje f-je P, Q, R kao podintegralne izraze
∫ po proizvoljnoj liniji dl i ∫ po njome zahvaćenoj površini dS

∫

L Pdx + Qdy + Rdz =

∫

S ﴾

∂R

−

∂Q

﴿ dydz +  ﴾

∂P

−

∂R

﴿ dzdx +  ﴾

∂Q

−

∂P

﴿ dxdy

∂y

∂z

∂z

∂x

∂x

∂y

Prostorni izvod funkcije polja nastaje kada površ integracije S teži ka tački M₀,
odnosno njome obuhvaćena zapremina V_S teži nuli.

Prostorni izvod funkcije polja ima tri oblika, u zavisnsoti od podintegralnog izraza φ(r_v) • dσ_v
u slučaju da je φ(x,y,z) skalarna funkcija položaja izraz izvoda će biti vektor

lim	Ip	= ▼φ(x,y,z) =	∂φ	i +	∂φ	j +	∂φ	k	= grad φ
VS → 0	VS		∂x		∂y		∂z

u slučaju da je v_v(r_v) vektorska funkcija položaja a izraz izvoda skalarni proizvod f-je i orijentisanog elementa površi: v_v • dσ_v
izraz izvoda će biti skalar

lim	Ip	= ▼ • vv(x,y,z) =	∂v1	+	∂v2	+	∂v3		= div vv
VS → 0	VS		∂x		∂y		∂z

u slučaju da je v_v(r_v) vektorska funkcija položaja a izraz izvoda vektorski proizvod f-je i orijentisanog elementa površi: dσ_v × v_v
izraz izvoda će biti vektor

lim	Ip	= ▼ × vv(x,y,z) = ﴾	∂	i +	∂	j +	∂	k﴿ × ﴾	v1 i + v2 j + v3 k ﴿ = rot vv
VS → 0	VS		∂x		∂y		∂z

prema uobičajenom postupku za vektorski proizvod biće:

rot vv =

i

j

k

= ﴾

∂v3

−

∂v2

﴿ i +  ﴾

∂v1

−

∂v3

﴿ j +  ﴾

∂v2

−

∂v1

﴿ k

∂

∂

∂

∂x

∂y

∂z

∂y

∂z

∂z

∂x

∂x

∂y

v1

v2

v3

---

drv= λ • vv (rv) ; λ= skalar ili   drv×vv (rv) = 0 linija vektorskog polja

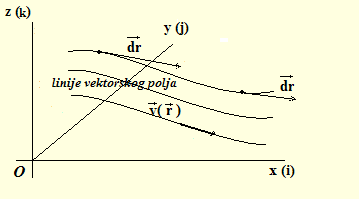
linija vektorskog polja je kriva linija u vektorskom polju čija je tangenta nosač vektora v_v(r_v).
A kada je dr_v orijentisani element tangente onda važi: dr_v= λ • v_v (r_v) ; λ= skalar   ili   dr_v×v_v (r_v) = 0 tj. orijentisani element i vektorska f-ja v_v su kolinearni
iz skalarnog proizvoda proizilazi: dx i + dy j + dz k = λ • (v₁ i + v₂ j + v₃ k) sledi: dx = λv₁ ; dy = λv₂ ; dz = λv₃

λ =	dx	=	dy	=	dz
	v1(x,y,z)		v2(x,y,z)		v3(x,y,z)

a iz vektorskog protizvoda proizilazi:

drv × vv =	i	j	k	= ( dyv3 - dzv2) i + (dzv1 - dxv3) j + (dxv2 - dyv1) k  = 0
	dx	dy	dz
	v1	v2	v3

vektroski proizvod kolinearnih vektora je 0, i njegove komponente po koordinatama su nule ( dyv₃ - dzv₂) = 0 ٨ (dzv₁ - dxv₃) = 0 ٨ (dxv₂ - dyv₁) =0

dy	=	v2	;	dz	=	v3	;	dx	=	v1
dz		v3		dx		v1		dy		v2

---

rot vv (rv) × drv vrtložne linije

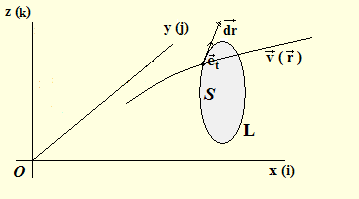
vrtložna linija u vektorskom polju je kriva linija čija je tangenta u svakoj tački nosač rotora vektora v_v.
Ako je dr_v orijentisani element ove krive, onda je rot v × dr_v = 0 jer su vektori kolinearni.
Kada se vektor rot v prikaže kao zbir komponeneti: rot v_v = r₁ i + r₂ j +r₃ k, a dr_v = dx i + dy j + dz k.
Iz definicije rotora sledi

r1 = ﴾

∂v3

−

∂v2

﴿   r2 =  ﴾

∂v1

−

∂v3

﴿   r3 =  ﴾

∂v2

−

∂v1

﴿

∂y

∂z

∂z

∂x

∂x

∂y

Polazeći od gornjeg izraza za rot v i dr možemo pisati:

rot v × dr = 0
(r₁ i + r₂ j +r₃ k) × (dx i + dy j + dz k) = (r₂dz − r₃dy ) i + (r₃dx − r₁dz) j + (r₁dy − r₂dx) k = 0
Vektorski proizvod kolinearnih vektora ima sve komponente 0 pa je:
(r₂dz − r₃dy ) = 0 ٨ (r₃dx − r₁dz) = 0 ٨ (r₁dy − r₂dx) = 0 odatle sledi:

dz

=

dy

;

dx

=

dz

;

dy

=

dx

;

r3

r2

r1

r3

r2

r1

Vrtložne linije su integralne krive sistema diferencijalnih jednačina:

dx	=	dy	=	dz
r1		r2		r3

Smenom iz def. komponenti za rot v_v biće:

dx	=	dy	=	dz
∂v3  −  ∂v2 ∂y ∂z		∂v1  −   ∂v3 ∂z ∂x		∂v2  −  ∂v1 ∂x ∂y

---

∫ L vv (rv) • drv = rad vektorske f-je

rad vektora u vektorskom polju vektora v_v (r_v) duž krive, čiji je ort e_t tangente u smeru u kom lukovi rastu.
Kada je kriva zatvorena on se zove i još cirkulacija vektora
Skalarni proizvod v_v (r_v) • e_t je ortogonalna projekcija vektora v_v na orijentisanu tangentu krive dr_v
∫ _L v_v(v₁, v₂, v₃) • dr_v = ∫ _L v_v • e_tdl = ∫ _L ﴾ v₁e₁ + v₂e₂ + v₃e₃ ﴿ dl = ∫ _L v₁dx + v₂dy + v₃dz
Stoksova formula između ∫ po liniji i ∫ po obuhvaćenoj površini daje:

∫ L v1dx + v2dy + v3dz =

∫ S

﴾

∂v3

−

∂v2

﴿ e1 +  ﴾

∂v1

−

∂v3

﴿ e2 +  ﴾

∂v2

−

∂v1

﴿ e3

dS

∂y

∂z

∂z

∂x

∂x

∂y

∫ L vv(v1, v2, v3) • drv =

∫ S

﴾

∂v3

−

∂v2

﴿ i +  ﴾

∂v1

−

∂v3

﴿ j +  ﴾

∂v2

−

∂v1

﴿ k

• dσv    jer je edS = dσv

∂y

∂z

∂z

∂x

∂x

∂y

rad vektora po krivoj L jednak je rotoru vektorske f-je po obuhvaćenoj površini S

∫ _L v_v • dr_v = ∫ _S rot v_v • dσ_v

---

∫ S vv (rv) • dσv = fluks vektorske f-je

fluks vektora je "proticanje" u vektorskom polju vektora v_v(r_v) kroz površ S, čiji je ort e_n u smeru spoljne normale na tu površ.
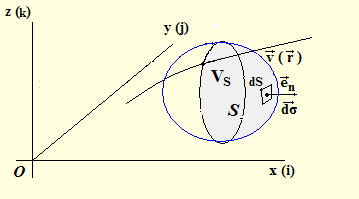
Skalarni proizvod v_v (r_v) • e_n je ortogonalna projekcija vektora v_v na orijentisanu normalu površine S.

∫

S vv • dσv =

∫

S vv • edS =

∫

S ﴾ v1e1 + v2e2 + v3e3 ﴿ dS =

∫

S v1 · e1dS + v2 · e2dS + v3 · e3dS

A prema formuli Ostrogradskog:

∫	S v1dydz + v2dzdx + v3dxdy =	∫	VS ﴾	∂v1	+	∂v2	+	∂v3	﴿ dV
				∂x		∂y		∂z

Fluks vektora kroz određenu površinu S, jednak je divergenciji vektorske f-je kroz površinom obuhvaćenu zapreminu V_S.

∫ _S v_v • dσ_v = ∫ _VS div v_v · dV

---

Klasifikacija vektorskih polja
Elementi klasifikacije polja skalarne funkcije φ(x,y,z) i vektorske funkcije v_v( r_v) = v₁ i + v₂ j + v₃ k su:

grad φ =	∂φ	i +	∂φ	j +	∂φ	k
	∂x		∂y		∂z

div vv =	∂v1	+	∂v2	+	∂v3
	∂x		∂y		∂z

rot vv =

﴾

∂v3

−

∂v2

﴿ i +  ﴾

∂v1

−

∂v3

﴿ j +  ﴾

∂v2

−

∂v1

﴿ k

∂y

∂z

∂z

∂x

∂x

∂y

elmenti	grad φ	div vv	rot vv	naziv	komentar
vrednosti el.	=	≠ 0	= 0	bezvrtložno    čisto izvorno	tačke sa div vv > 0 su izvori polja a tačke sa div vv < 0 su ponori polja ili negativni izvori iz rot v =0 → v = grad φ , gradijentsko polje, potencijalno polje
	-	= 0	≠ 0	bezizvorno-solenoidno    čisto vrtložno	tačke sa div vv = 0 su bezizvorni delovi polja kako je rot vv <> 0 onda je čisto vrtložno polje
	-	= 0	= 0	Laplasovo	iz div v = 0 je bezizvorno, skalarno potencijalno polje a iz rot v = 0 je bezvrtložno
	-	≠ 0	≠ 0	složeno	složeno polje nastaje superpozicijom jednog potencijalnog vvp polja i jednog solenoidnog vvs polja vv = vvp + vvs gde je div vvp = α  a  rot vvp = 0 i div vvs = 0  a  rot vvs = β pa je i div vv = div (vvp + vvs) = div vvp + 0 = α isto tako rot vv = rot (vvp + vvs) = 0 + rot vvs = β

---

IZVORI
Dr. Radivoje Kašanin, viša matematika II, Naučna knjiga, Beograd 1950
Dr. Dobrivoje Mihailović, Elementi vektorske analize, difer. geometrije i teorije polja, ZIU, Beograd 1968
Dr. Milorad Bertolino, Opšti kurs matematike, ICS, Beograd 1974
i još ______________________________
Tatomir P. Anđelić, Tenzorski račun, Naučna knjiga, Beograd 1952
L. P. Ajzenhart, Uvod u difer. geometriju, Naučna knjiga, Beograd 1951



  Na početak!  

---

This is a part of CaDu-famili OpSo Intelectual Project
Open Source Licence  © July, 2015. ver. 1.0